4.2 Waves
Joey Zhuang, Khoi Tran, Gurdit Sood
Electronic Transition - Absorption and Emission Spectra
In Bohr’s model of hydrogen, there is only a fixed set of orbits than an electron can move in (n = 1, 2, 3, etc.). As electrons absorb energy from external sources, they can “jump” from a lower orbit to a higher orbit. In this process, it is said that the electrons are excited. When they fall back down to lower levels, they emit discrete amounts of energy.
Because energy is quite relative, we define the orbital of “zero energy” as an orbital that is infinitely far from the nucleus. It was also established that the energy level of each orbit decreases the closer they are to the nucleus, and that this energy is inversely proportional to the square of the orbit number. Therefore,
$$E = \frac{-R_H}{n^2}\ (1)$$
where $R_H$ is the Rydberg constant for energy of hydrogen, $R_H = 2.17868 \cdot 10^{-18} \text{J}$.
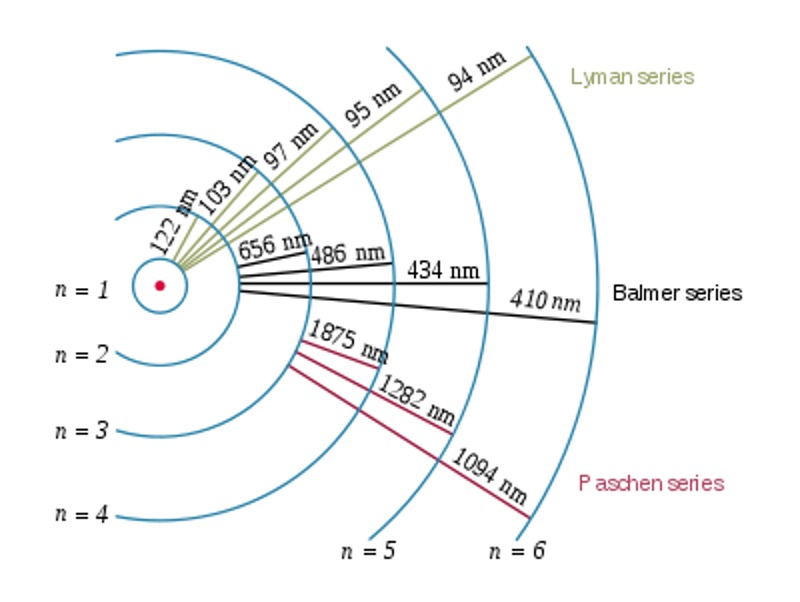
Figure 1: Electron transitions and wavelengths of emitted EM radiation for hydrogen.2
Ionization Energy
The amount of energy required to remove an electron from an atom (which is hydrogen in this case) is called the ionization energy. Because the removal of an electron can be seen as the excitation of a ground-state electron (n = 1) to infinitely far away (n = ∞), the ionization energy must be equal to the change in energy of the electron due to the law of conservation of energy.
$$I = \Delta E = E_{∞} - E_1 = \lim_{n \to \infty} [-R_H (\frac{1}{n^2} - \frac{1}{1^2})] = R_H = 2.17868 \cdot 10^{-18}$$
Note that we can also apply the same principle in the calculation of the energy required from a photon to excite an electron from an energy level to another:
$$E_{\text{photon}} = h\nu = \Delta E = E_{\text{upper}} - E_{\text{lower}}$$ $$= -R_H (\frac{1}{n_{\text{upper}}^2} - \frac{1}{n_{\text{lower}}^2} = R_H (\frac{1}{n_{\text{lower}}^2} - \frac{1}{n_{\text{upper}}^2})\ (2)$$
However, equation (2) only applies to a hydrogen atom. Fortunately, we can adjust the equation for other hydrogen-like atoms (atoms with one electron):
$$\Delta E = Z^2 R_H (\frac{1}{n_{\text{lower}}^2} - \frac{1}{n_{\text{upper}}^2})\ (3)$$
where Z is the nuclear charge of the atom.
The energy calculated using equation (3) equals to the energy of the electromagnetic radiation emitted when the electron falls to a lower energy level (electronic relaxation), or the energy absorbed so that the electron “jumps” to a higher energy level (electronic excitation).
Wave-Particle Duality
The photoelectric effect describes the observation that when light hits the surface of specific metals, electrons are ‘ejected’ from the surface. Thus, light seems to behave like particles. However, when light passes through different mediums (e.g., from air through glass), it changes directions. This is a wave-like behaviour. And so light has a dual nature; it behaves as both particles and waves. However, this idea does not only apply to light but also to particles of matter and electrons (i.e., small particles of matter and electrons can behave as both a particle and a wave)
Since light, matter, and electrons behave as particles, the wavelength ($\lambda$) of either light, matter, or an electron can be described by the equation: $\lambda = \frac{h}{mu}$.
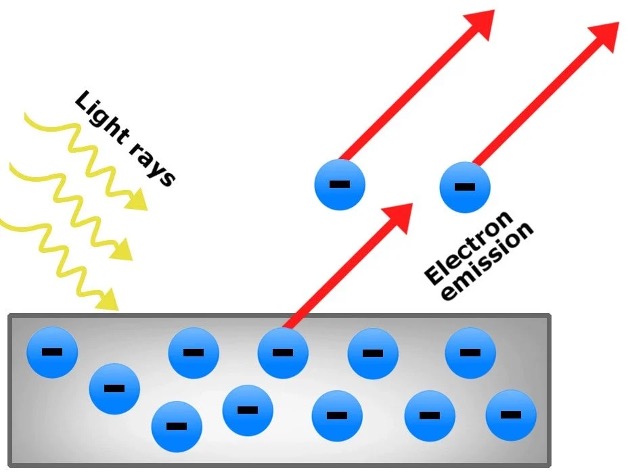
Figure 2: The Photoelectric Effect.3
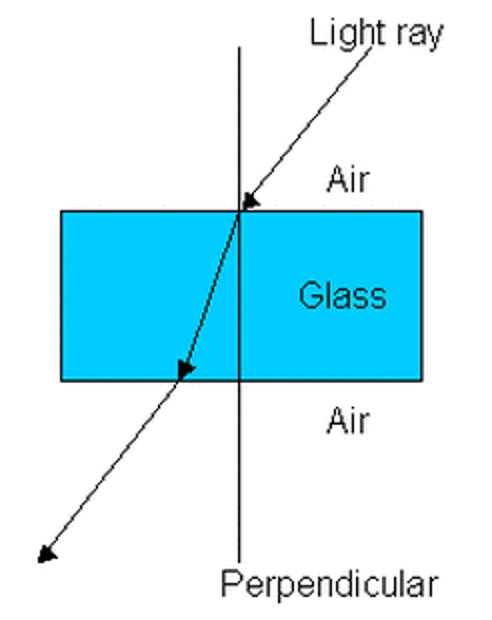
Figure 3: Light as a wave bending through different mediums.4
Since light, matter, and electrons behave as particles, the wavelength ($\lambda$) of either light, matter, or an electron can be described by the equation: $\frac{h}{mu}$. This is called De Broglie’s equation, and it can be derived from what we covered previously in this module.
Let’s first consider a photon: $$E = h\nu$$
Using Einstein’s famous equation from relativity, we can combine and rearrange the equation to describe the momentum of a photon: $$E = mc^2$$ $$h\nu = mc^2$$ $$\frac{h\nu}{c} = mc$$
Furthermore, from what we learned about electromagnetic radiation, we know that: $$c = \nu \lambda$$
Therefore, we can substitute this in for c in the equation for the momentum of a photon, and complete the derivation: $$\frac{h\nu}{\nu \lambda} = mc$$ $$\frac{h}{\lambda} = mc$$ $$\lambda = \frac{h}{mc}$$
Finally, $c$ represents the velocity of the photon. However, this equation can be used for any object, so $c$ and be replaced with $u$ to represent the velocity of any object. To reiterate, this equation is significant because it shows that matter has wavelengths, just like light. In summary,
$$\lambda = \frac{h}{mu}$$
Where:
- $\lambda$ = wavelength in meters
- $u$ = velocity in meters/second
- $m$ = mass in kilograms
- $h$ = Planck’s constant = $6.63 \cdot 10^{-34} \text{J s}$
Uncertainty Principle
The Heisenberg uncertainty principle states that the precise position ($\Delta x$) and momentum ($\Delta p$) of a particle cannot be known simultaneously. The uncertainties of both the position and momentum of a particle is: $\Delta x \Delta p \geq \frac{h}{4\pi}$.These uncertainties in the particle’s position and momentum are due to a particle’s wave-like behaviour.
Figure 4: Characteristics of a wave.5
A wave is a standing wave when they have these characteristics:
- There is no displacement at the fixed ends and nodes (i.e., the amplitude is 0)
- The crests and troughs of the waves occur at the same positions (e.g., 5 and -5 on a graph respectively)
- The wave vibrates in the region between the crests and troughs
Figure 5: Standing wave showing characteristics and nodes.6
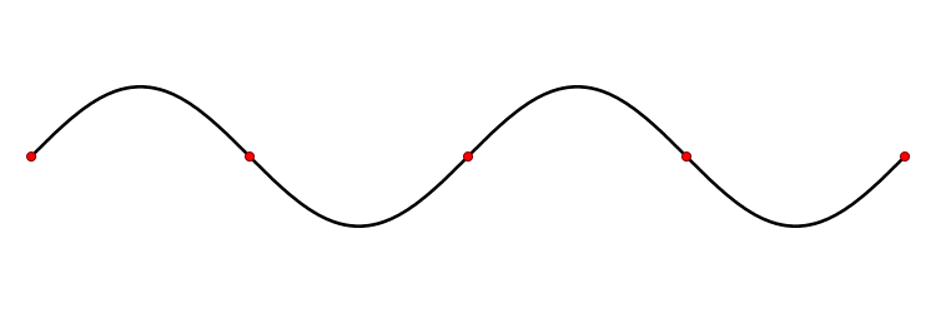
Figure 6: Standing wave in action.7
Wave Function
Particle in a Box
Since we have established that matter can also have wavelike properties, their wavelike characteristics could be described by a mathematical equation known as a wave function. Erwin Schrödinger in 1927 had suggested this exact idea for electrons/particles. The symbol for the wave function is “psi” ($\psi$).
But why do we care? Well, there is no proper definition for what actually is, however, interpreting the wave function is quite useful for us. In particular, if you square the wave function ($\psi^2$), it gives the probability of finding a particle in a specific space.
Let’s take a step back, and just look at $\psi$. Imagine a particle that is enclosed in a one-dimensional box, only able to move in one direction. Due to the particle being enclosed in the box, so are its waves, creating a standing wave of the particle in this 1-D box. Remember quantization of energy? Well, each wave has a specific energy associated with it, as can be seen in Figure 7.
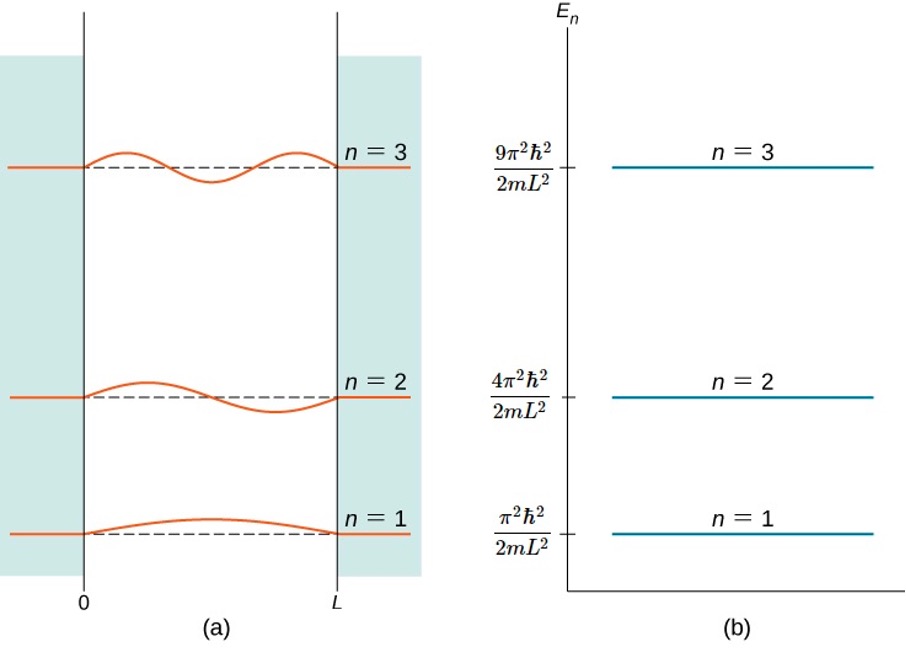
Figure 7: Different wave functions.8
Understanding $\psi^2$
Now that we understand the phenomenon of the particle in a box, let’s take a look at why all this really matters. Using the particle-in-a-box model we just learned, now let’s apply that to a three-dimensional space.
The probability of finding an electron in a 3-D space cannot be determined by one quantum number “n”, as the particle moves in 3 different directions instead of 1 direction in 1-D. So if we had designated movement of the particle in 1-D as “x”, then for 3-D, it can be denoted by x, y, and z, each representing a different direction. Thus, for three different directions, we would need 3 different quantum numbers.
Additionally, know that for every point where $\psi^2$ = 0, that is known as a node and that indicates that there is no probability of finding the particle in that region.
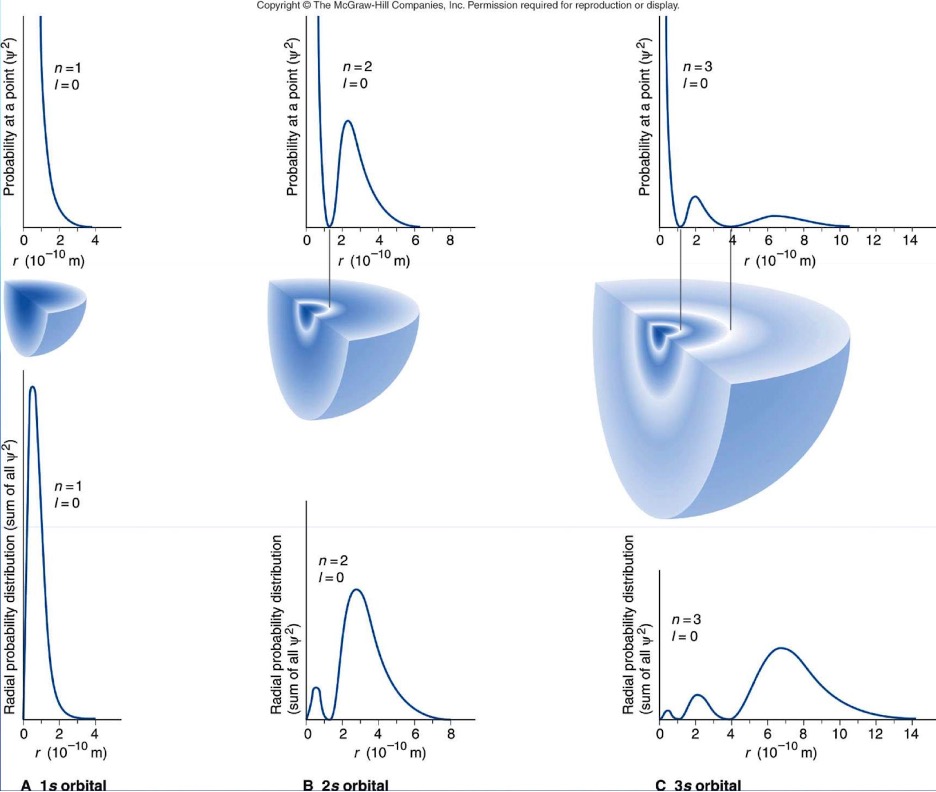
Figure 8: Different wave functions.9
Practice Problems
When performing experiments with malfunctioning equipment in his lab, Bunatoli Agorski got into an accident in which a high-energy proton beam from a particle accelerator passed through his brain (and miraculously survived). Given that the protons in the particle accelerator moved at 98% the speed of light with 1% uncertainty, what was the uncertainty in the position of the protons?
The wavelengths of the electromagnetic radiation emitted as the electron of a hydrogen-like atom falls to the ground state are plotted, with the wavelength increasing from left to right on the x-axis. If the leftmost spectral line has a wavelength of 22.8 nm,
a. What is the one-electron species?
b. What is the wavelength of the fourth line from the right?
What is the de Broglie wavelength of a soccer ball with a mass of 412 g and velocity of 83.2 km/h?
An electron is travelling with a kinetic energy of $1.3616 \cdot 10^{-16} J$. Calculate its wavelength.
References
Petrucci RH, Herring FG, Madura JD, Bissonnette C. General Chemistry: Principles And Modern Applications. 11th ed. Toronto, ON: Pearson Canada; 2017:317-328.
Electron Shell Transitions Of Hydrogen.; 2022. https://commons.wikimedia.org/wiki/File:Hydrogen_transitions.svg. Accessed September 13, 2022.
What is the Photoelectric Effect?. Science ABC. https://www.scienceabc.com/pure-sciences/what-explain-photoelectric-effect-einstein-definition-exmaple-applications-threshold-frequency.html. Published 2022. Accessed July 7, 2022.
Hoang, Lovatt. Scientific Explanation. The Refraction of Light. https://therefractionoflight.weebly.com/scientific-explanation.html. Published 2013. Accessed July 7, 2022.
Wave characteristics review (article) | Khan Academy. Khan Academy. https://www.khanacademy.org/science/high-school-physics/waves-and-sound/wave-characteristics/a/wave-characteristics-review-ap-physics-1. Accessed July 7, 2022.
Enevoldsen K. Standing Waves in Strings. Thinkzone.wlonk.com. https://thinkzone.wlonk.com/StandingWaves/StandingWavesInStrings.htm. Published 2019. Accessed July 8, 2022.
Vieira L. Standing Wave.; 2004. https://commons.wikimedia.org/wiki/File:Standing_wave.gif. Accessed September 2, 2022.
Libretexts. 3.6: The energy of a particle in a box is quantized. Chemistry LibreTexts. https://chem.libretexts.org/Courses/University_of_California_Davis/UCD_Chem_110A%3A_Physical_Chemistry__I/UCD_Chem_110A%3A_Physical_Chemistry_I_%28Larsen%29/Text/03%3A_The_Schrodinger_Equation_and_the_Particle-in-a-Box_Model/3.06%3A_The_Energy_of_a_Particle_in_a_Box_is_Quantized. Published October 11, 2021. Accessed July 16, 2022.
Draper S. Visualization Of Electron Distribution Of Different S Orbitals. https://chemistry.tcd.ie/staff/people/sd/lectures/MO_lecture_course-2.pdf. Accessed September 17, 2022.