4.1 Quantum mechanics
Khoi Tran
Introduction to Quantum Mechanics
While classical mechanics, which you probably learned in middle school or high school, is used to describe the behavior of larger objects, quantum mechanics focuses on small particles (like subatomic kind of small).
We would probably all agree that things that we see everyday (e.g., your desk, a water bottle, a basketball) are made up of particles (unless you and your friend drank too much last night). However, in quantum mechanics, things are a bit different. All objects are both a particle and a wave, and this property is particularly significant for sub-atomic objects. For example, electrons are not simply little negatively-charged balls that hang around the nucleus, but they should be seen as a negatively charged cloud that spreads out to infinity.
In movies, quantum mechanics is usually blamed for anything scientifically complicated because film directors cannot wrap their heads around the idea that their water bottle is both a particle and a wave. Trust me, quantum mechanics is not necessarily that daunting.
Electromagnetic Radiation
Electromagnetic (EM) wave is a type of wave that contains electric and magnetic fields perpendicular to each other (you do not need to know how this works). Common types of electromagnetic radiation include light, radio waves, x-ray, etc. All electromagnetic waves move through vacuum at the speed of light, c.
Similar to any wave (Figure 1), EM waves can be represented by their wavelength λ (in meters) and frequency ν (in Hertz, Hz, which is equal to s-1). The speed of EM waves equals to the number of wavelengths that pass through a point every second, and therefore equals to wavelength times frequency:1
Note: in the equation above is the Greek letter ‘nu’ (pronounced ‘new’). Please do not pronounce it ‘vee’ as it hurts the feelings of everyone in the Chemistry and Physics Departments.
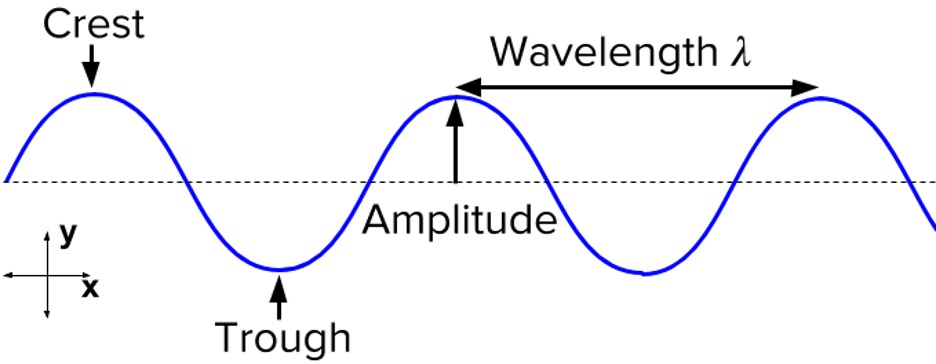
Figure 1: Properties of a wave2
Quantization of Energy
In order to fully explain a phenomenon called the blackbody radiation, a German scientist with a cool mustache named Max Planck established that EM waves all have a limit to how little energy they can carry. The smallest amount of energy that an EM wave can contain is called a quantum.
In other words, an EM wave can carry 1 quantum, 2 quanta, 3 quanta, etc. of energy and so on, but energy can never be transmitted in fractions of a quantum (e.g., 1.25 quanta, 1.5 quanta). Through experiments, Max Planck showed that the energy of a quantum is directly proportional to the frequency (nu) of the wave: where is the energy of a quantum, and is a proportionality constant.1
Later on, Planck was able to calculate the proportionality constant to be equal to , and is known as Planck’s constant.
Note: Planck’s quantum theory explains the blackbody radiation by combining with Boltzmann’s equation to show that high energy waves are extremely unlikely to be emitted and therefore the energy emitted is finite. However, this is beyond the scope of CHEM112 so do not waste time trying to understand how it works.
The Photoelectric Effect
It was observed that electrons are ejected from the surface of certain metals when they are struck with light. This phenomenon is known as the photoelectric effect. However, ejection of electrons is only observed when the incident light exceeds a specific frequency (i.e., changing the intensity of the light does not cause electrons to be emitted). Furthermore, when the threshold frequency is met:
- Increased intensity of the incident light leads to more electrons being ejected.
- Increased frequency of the incident light increases the kinetic energy of emitted electrons.
Classical wave theory at the time failed to provide sufficient explanations for these observations. However, in 1905, another German scientist with another cool mustache named Albert Einstein proposed that quanta of light (and EM waves in general) have particle-like properties. Quanta of light would later be termed photons. The energy of photons is also given by the following equation:
If we see photons as balls striking a surface, increased frequency is analogous to increased kinetic energy of the balls. As the balls hit the surface, electrons will be struck off at higher kinetic energy. Increased intensity is similar to more balls striking the surface; more electrons will be ejected at the same kinetic energy.
The energy binding the electrons to the surface is called the work function (ϕ). In order to eject electrons off the surface, incoming energy must be equal to or greater than ϕ, and any excess energy will appear as kinetic energy of the ejected electrons. This is consistent with the law of conservation of energy.
Atomic Spectra
Because energy is quantized, electrons of an atom can only absorb specific amounts of energy and “jump” to concrete energy levels. As electrons “jump” to higher energy levels, the atom is said to be in an excited state. When the electrons fall back to lower energy levels, EM radiation is emitted. Emitted EM radiation at specific wavelengths are within the visible light spectrum and can be seen on atomic spectra as concrete coloured lines at certain wavelengths.
For example, the wavelengths of EM radiation emitted when the electron of a hydrogen atom falls to lower energy levels are illustrated in Figure 2 below. The series of spectral lines emitted by hydrogen when the electron falls to n = 1, n = 2, and n = 3 are called Lyman series, Balmer series, and Paschen series, respectively.
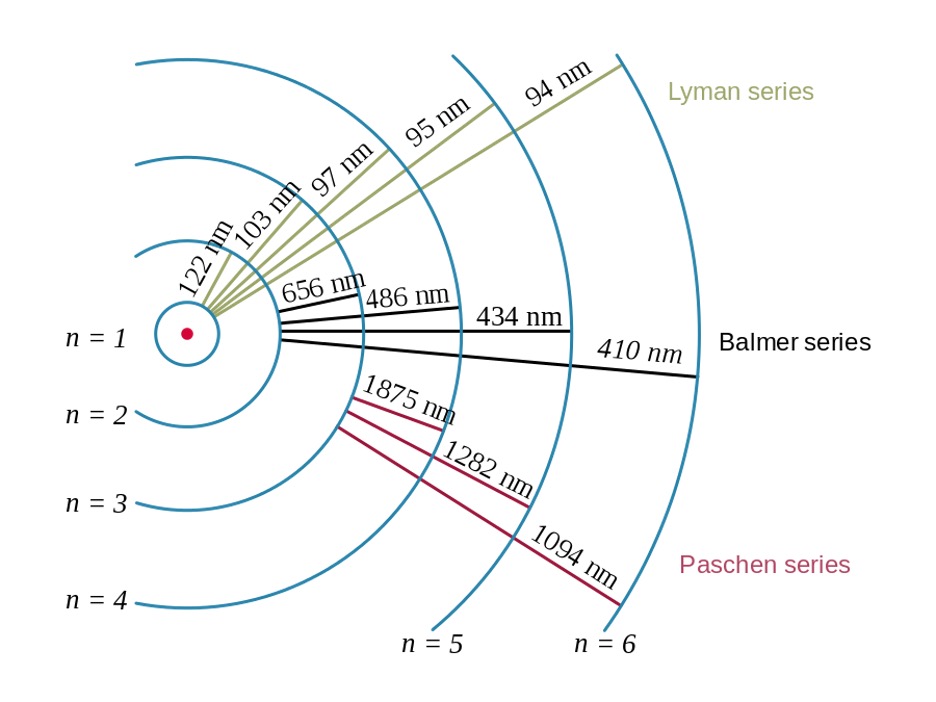
Figure 2: Electron transitions and wavelengths of emitted EM radiation for hydrogen3
Practice Problems
What is the energy of an X-ray with a wavelength of 1.0 nm per quantum?
In an experiment with the photoelectric effect, Dr. Plax Manck shines light on a metal surface with a work function of 4.94*10-19 J. What is the speed of the electron ejected if the wavelength of the light used is a) 340 nm? b) 850 nm?
As electrons fall to lower energy levels, energy is emitted in the form of electromagnetic radiation, which may or may not be visible to the human eye. For neutral atoms with one valence electron, the wavelength of the electromagnetic radiation emitted is dependent on the element’s atomic number and the principal quantum numbers of the higher and lower energy levels.
This is shown in the Rydberg formula below:
Where R is the Rydberg constant, Z is the atomic number, and n1 and n2 are the lower and higher principal quantum numbers, respectively.
Dr. Einbert Alstein experimentally determines that the spectral line of hydrogen with the second-highest wavelength of the Balmer series has a wavelength of 493.0 nm.
a) Calculate the experimental value for the Rydberg constant for hydrogen with correct units.
b) Based on your result from part a, what is the shortest possible wavelength an excited hydrogen atom can emit?
References
Petrucci RH, Herring FG, Madura JD, Bissonnette C. General Chemistry: Principles And Modern Applications. 11th ed. Toronto, ON: Pearson Canada; 2017:302-317.
Khan Academy. Parts Of A Transverse Wave (Image); 2022. https://www.khanacademy.org/science/in-in-class11th-physics/in-in-11th-physics-waves/in-in-wave-characteristics/a/wave-characteristics-review-ap-physics-1. Accessed September 13, 2022.
Electron Shell Transitions Of Hydrogen.; 2022. https://commons.wikimedia.org/wiki/File:Hydrogen_transitions.svg. Accessed September 13, 2022.